In mathematics, the Lambert W function, also called the omega function or product logarithm, is a set of functions, namely the branches of the inverse relation of the function f(w) = wew where ew is the exponential function and w is any complex number. In other words, the defining equation for W(z) is
Since the function ƒ is not injective, the relation W is multivalued (except at 0).
Multivalued.
Main branch of the Lambert W function in the complex plane.
Kompleksinė paišyba.
Lambert first considered the related Lambert's Transcendental Equation in 1758, which led to a paper by Leonhard Euler in 1783 that discussed the special case of wew. However the inverse of wew was first described by Pólya and Szegő in 1925. The Lambert W function was "re-discovered" every decade or so in specialized applications but its full importance was not realized until the 1990s. When it was reported that the Lambert W function provides an exact solution to the quantum-mechanical double-well Dirac delta function model for equal charges—a fundamental problem in physics—Corless and developers of the Maple Computer algebra system made a library search to find that this function was in fact ubiquitous to nature.
Пример:
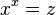

следовательно,

Kaip tai dera su "this function was in fact ubiquitous to nature"?

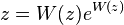





Komentarų nėra:
Rašyti komentarą